Towards the Interpretability Logic of all Reasonable Arithmetical Theories

Joost J. Joosten

12 december 1998

Abstract:

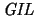
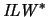
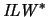
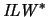
The subject of this paper is the interpretability logic of all reasonable arithmetical theories, which we baptize $\mathit{GIL}$. This logic has long been conjectured by Albert Visser to be $\mathit{ILW}^*$. No modal completeness result was known for $\mathit{ILW}^*$. In order to provide a completeness proof of $\mathit{ILW}^*$, a good understanding of the sublogic $\mathit{ILM_0}$ seems indispensable. But there was no modal completeness result for $\mathit{ILM_0}$ either. In this paper a method for constructing models is developed. By this model-construction method we obtain a new proof of the modal completeness and decidability of $\mathit{ILM}$. 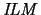Moreover do we obtain the modal completeness of $\mathit{ILM_0}$. Furthermore, a new principle, P₀, is introduced and studied. This principle is seen to be arithmetically valid and is completely independent with regard to the other principles studied here. 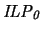The new logic $\mathit{ILP_0}$ turns out to be modally incomplete. 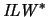The conjecture of $\mathit{ILW}^*$ being the interpretability logic of all reasonable arithmetical theories is thus falsified.