



Next: The actual construction.
Up: Deficiencies
Previous: Deficiencies
We now prove by induction on the number of possible deficiencies that
every deficiency in x w.r.t. y can be eliminated in an adequate
way. (For the time being we only consider the harder case when
intermediate worlds do exist.) Adequate means that all the Sxsuccessors of y that are defined for this purpose contain all the
 -formulas of x' (
xReBx'Ry). The new worlds should not
provoke new deficiencies in x. And all of them should lie
B-critically above x.
-formulas of x' (
xReBx'Ry). The new worlds should not
provoke new deficiencies in x. And all of them should lie
B-critically above x.
-
If you only have
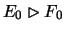 as possible deficiency in x and this
is indeed a deficiency, i.e.
as possible deficiency in x and this
is indeed a deficiency, i.e. 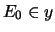 ,
you can apply lemma
5.4. This yields a y' such that
,
you can apply lemma
5.4. This yields a y' such that
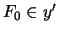 ,
,
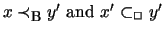 .
This y is taken to
be maximal w.r.t. the
.
This y is taken to
be maximal w.r.t. the  -inclusion. You can thus safely define
ySxy' and no new deficiencies will emerge in x w.r.t. y, for
they have to be amongst the possible deficiencies. The model is closed
under the frame conditions.
-inclusion. You can thus safely define
ySxy' and no new deficiencies will emerge in x w.r.t. y, for
they have to be amongst the possible deficiencies. The model is closed
under the frame conditions.
-
If the possible deficiencies are
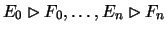 ,
one can make use of lemma 5.5 to derive n! useful
sentences. Also the corresponding set
,
one can make use of lemma 5.5 to derive n! useful
sentences. Also the corresponding set
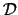 is formed by the
same method as before. Let again
is formed by the
same method as before. Let again
 be
all the F's that do not occur as such in
be
all the F's that do not occur as such in
 .
Lemma
5.6 guarantees the existence of a subset
.
Lemma
5.6 guarantees the existence of a subset
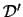 which has, for every Fj that occurs in
which has, for every Fj that occurs in
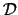 ,
one disjunct
that contains both Fj and
,
one disjunct
that contains both Fj and
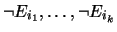 .
For every disjunct in
.
For every disjunct in
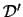 a corresponding world
can be found where that very disjunct holds. This world will also lie
B-critically above x.
a corresponding world
can be found where that very disjunct holds. This world will also lie
B-critically above x.
But one does not meet all the requirements
like this. For the worlds only contain a finite part of the box
formulas in x', namely the 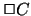 that was included in all the
n! formulas. This calls for compactness again. Let
that was included in all the
n! formulas. This calls for compactness again. Let
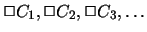 be an enumeration of all the box formulas in
x'. Let
be an enumeration of all the box formulas in
x'. Let
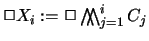 .
For every
.
For every 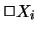 a set
a set
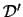 as above is formed. As
only a finite number of partitions is possible for
as above is formed. As
only a finite number of partitions is possible for
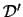 ,
one
specific partition must show up infinitely many times. With respect to
every individual world of this (or better corresponding to this)
partition the compactness theorem can be applied to obtain a set of
worlds. All of these worlds will contain some Fj, all of
,
one
specific partition must show up infinitely many times. With respect to
every individual world of this (or better corresponding to this)
partition the compactness theorem can be applied to obtain a set of
worlds. All of these worlds will contain some Fj, all of
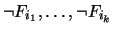 ,
and all the
,
and all the
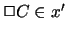 .
They can
also be taken maximal w.r.t.
.
They can
also be taken maximal w.r.t.  -inclusion. This set of worlds is called
-inclusion. This set of worlds is called
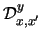 .
So
.
So
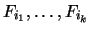 do not occur in
do not occur in
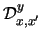 .
For these
remaining k possible deficiencies you can apply the induction
hypothesis while ignoring the n-k+1 other possible
deficiencies. Note that if k=n+1 the whole situation becomes very
trivial. So, without loss of generality, we can assume that k < n+1. Applying the induction hypothesis yields a whole net of
B-critical successors of x solving all the k deficiencies
disregarding the other n-k+1 possible deficiencies. Every world in
this net contains all the
.
For these
remaining k possible deficiencies you can apply the induction
hypothesis while ignoring the n-k+1 other possible
deficiencies. Note that if k=n+1 the whole situation becomes very
trivial. So, without loss of generality, we can assume that k < n+1. Applying the induction hypothesis yields a whole net of
B-critical successors of x solving all the k deficiencies
disregarding the other n-k+1 possible deficiencies. Every world in
this net contains all the  -formulas of x'. All the individual
members of this net are maximal w.r.t.
-formulas of x'. All the individual
members of this net are maximal w.r.t.  -inclusion. By
``attaching'' this B-critical net to y, k deficiencies are
solved but some deficiencies among the other n-k+1 possible ones may
``have become active''. You eliminate these deficiencies by defining
an Sx arrow from every world in the B-critical net to every world
in
-inclusion. By
``attaching'' this B-critical net to y, k deficiencies are
solved but some deficiencies among the other n-k+1 possible ones may
``have become active''. You eliminate these deficiencies by defining
an Sx arrow from every world in the B-critical net to every world
in
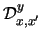 .
Sx on
.
Sx on
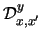 is defined
such that
is defined
such that
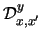 is completely Sx-connected. After
having done so, no deficiency in x remains w.r.t. any of the newly
defined worlds. If
is completely Sx-connected. After
having done so, no deficiency in x remains w.r.t. any of the newly
defined worlds. If
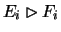 belongs to the group of k it is,
if necessary, eliminated in the B-critical net. If
belongs to the group of k it is,
if necessary, eliminated in the B-critical net. If
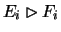 belongs to the group of n-k+1, there is always an Sx-arrow to a
world in
belongs to the group of n-k+1, there is always an Sx-arrow to a
world in
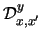 where Fi holds. In this world
Ej cannot hold for any
where Fi holds. In this world
Ej cannot hold for any
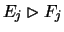 from the group of k. So
indeed all the deficiencies are eliminated. Moreover transitivity of
the Sx relation is guaranteed. The process described here will be
referred to as the process of making an Sxy-block.
from the group of k. So
indeed all the deficiencies are eliminated. Moreover transitivity of
the Sx relation is guaranteed. The process described here will be
referred to as the process of making an Sxy-block.
If there is a deficiency in x w.r.t. y and there is no
intermediate world, the situation becomes even easier. Again the
process of eliminating this deficiency in x w.r.t. y shall be
referred to as the process of making an Sxy-block. If in a general
setting the process of making an Sxy-block is mentioned, either
one of these two is meant, depending on the presence of intermediate
worlds. The process of making an Sxy-block in the case of no
intermediate worlds can inductively be described as follows.
-
Let y be in the Sxy-block.
-
begin As long as deficiencies in x exist w.r.t. some world
y in the Sxy-block, apply lemma 5.2 to obtain y''such that y'' resolves this deficiency by setting y'Sxy'' and
xRy''. As the whole Sxy-block is in at most one B-critical
cone of x, there is no ambiguity in applying lemma
5.2. Now make the whole Sxy-block completely Sx-connected.
end
As there is only a finite number of possible deficiencies, this
process must come to an end.




Next: The actual construction.
Up: Deficiencies
Previous: Deficiencies
Joost Joosten
2000-02-07