



Next: Eliminating deficiencies: the complete
Up: The construction
Previous: Problems
Again the deficiencies are harder to deal with. A first difficulty you encounter is in incorporating the
 -frame
condition. So, if you eliminate a deficiency in x w.r.t. y by
defining y Sx y', you should make sure that every possible
successor of y' can also be a successor of some intermediate x'
(intermediate means
x R x' R y). This is done, as stated
before, by demanding
-frame
condition. So, if you eliminate a deficiency in x w.r.t. y by
defining y Sx y', you should make sure that every possible
successor of y' can also be a successor of some intermediate x'
(intermediate means
x R x' R y). This is done, as stated
before, by demanding
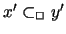 .
Lemma
5.4 tells us that this is indeed possible. So for every y''with
.
Lemma
5.4 tells us that this is indeed possible. So for every y''with
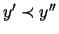 ,
you immediately have
,
you immediately have
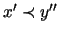 .
A closer
examination brings us to the second difficulty, that
is, that there might be more intermediate worlds between x and
y. But the invariant 6 tells us that there is always
an intermediate world that is maximal w.r.t. the
.
A closer
examination brings us to the second difficulty, that
is, that there might be more intermediate worlds between x and
y. But the invariant 6 tells us that there is always
an intermediate world that is maximal w.r.t. the  -inclusion
relation. This settles the second difficulty if we just apply lemma
5.4 every time to the
-inclusion
relation. This settles the second difficulty if we just apply lemma
5.4 every time to the  -maximal intermediate world.
A third difficulty is found when realizing that the
S-relation must be transitive. Say
-maximal intermediate world.
A third difficulty is found when realizing that the
S-relation must be transitive. Say 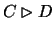 is a deficiency in
x w.r.t. y and we have
is a deficiency in
x w.r.t. y and we have
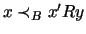 .
We want to create a
B-critical successor y' of x with
.
We want to create a
B-critical successor y' of x with 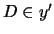 and
and
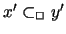 .
By doing so, every successor of y' can
automatically be defined a successor of x' and the
.
By doing so, every successor of y' can
automatically be defined a successor of x' and the
 -frame
condition is satisfied. Invariant 6 tells us that
without loss of generality we can take this x' to be maximal w.r.t. the
-frame
condition is satisfied. Invariant 6 tells us that
without loss of generality we can take this x' to be maximal w.r.t. the  -inclusion relation. Creating y' containing D, to
eliminate the deficiency
-inclusion relation. Creating y' containing D, to
eliminate the deficiency 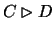 in x w.r.t. y is done in
such a way that
in x w.r.t. y is done in
such a way that
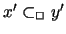 .
The existence of this
required entity is guaranteed by lemma 5.4. Automatically
we now have
.
The existence of this
required entity is guaranteed by lemma 5.4. Automatically
we now have
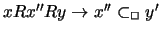 .
We
accordingly set y Sx y'. The general frame conditions demand x R
y'. Now it may happen that
.
We
accordingly set y Sx y'. The general frame conditions demand x R
y'. Now it may happen that
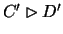 is a deficiency in xw.r.t. y'. It is easy to find a world y'' with D' in it and
being B-critical above x. The transitivity of Sx forces us to
also have y Sx y'', but by no means we can ensure that
is a deficiency in xw.r.t. y'. It is easy to find a world y'' with D' in it and
being B-critical above x. The transitivity of Sx forces us to
also have y Sx y'', but by no means we can ensure that
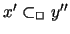 .
Somehow we have to relate the possible
deficiencies to each other. As we have only finitely many relevant
sentences of the form
.
Somehow we have to relate the possible
deficiencies to each other. As we have only finitely many relevant
sentences of the form 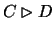 ,
the following lemma helps us out.
,
the following lemma helps us out.
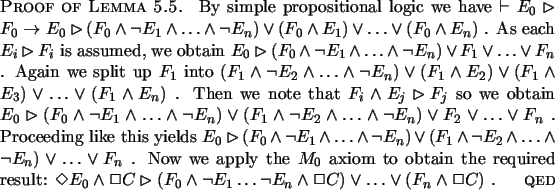
As the difference between the various Ei's is not essential, one
has the lemma for any permutation of the indices. If one encounters a
deficiency in x w.r.t. y, say
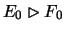 ,
one proceeds as
follows. First a list is made of all relevant sentences of the form
,
one proceeds as
follows. First a list is made of all relevant sentences of the form 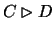 .
Let this list be
.
Let this list be
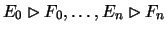 .
You can consider these as the possible deficiencies.
Let x' be such that
x R x' R y and
.
You can consider these as the possible deficiencies.
Let x' be such that
x R x' R y and
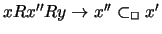 .
All deficiencies in x w.r.t. y will be eliminated in such a way
that no new deficiencies will occur in x w.r.t. the newly created
worlds. Again this process shall henceforth be referred to as the
process of making an Sxy-block. The
.
All deficiencies in x w.r.t. y will be eliminated in such a way
that no new deficiencies will occur in x w.r.t. the newly created
worlds. Again this process shall henceforth be referred to as the
process of making an Sxy-block. The  -inclusion of x' shall
be taken into account while creating this Sxy-block.
-inclusion of x' shall
be taken into account while creating this Sxy-block.
As stated before lemma 5.5 actually represents a manifold
of statements. All of them will be used in eliminating the deficiency
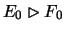 .
Let
.
Let 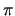 be a permutation of
be a permutation of
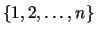 .
With any
.
With any 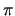 a series of sets
a series of sets
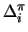 is defined.
is defined.
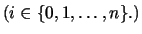
For the sake of convenience we define
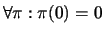 .
The notation
.
The notation
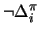 stands for the sentence
stands for the sentence
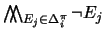 .
With this terminology one can easily
write down the n! useful variants of lemma 5.5.
.
With this terminology one can easily
write down the n! useful variants of lemma 5.5.
For any 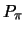 lemma 5.3 can be applied. Recall our situation,
x ReB x' R y with
lemma 5.3 can be applied. Recall our situation,
x ReB x' R y with
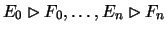 the
possible deficiencies in x w.r.t. y. So applying lemma 5.3
to any
the
possible deficiencies in x w.r.t. y. So applying lemma 5.3
to any 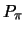 gives a maximal
gives a maximal
 -consistent set containing
one of the disjuncts of the consequent of
-consistent set containing
one of the disjuncts of the consequent of 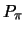 .
Note that
.
Note that
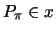 because
because
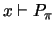 .
We now form a set of disjuncts
.
We now form a set of disjuncts
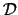 as follows. For every
as follows. For every 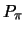 you choose the leftmost
disjunct of the consequent which is realizable by
applying lemmas 5.3 and 5.5.
you choose the leftmost
disjunct of the consequent which is realizable by
applying lemmas 5.3 and 5.5.
Lemma 5.6
Consider the above situation. Let
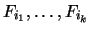
be all
the formulas that do not occur in any of the
n! disjuncts in
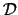
,
and let
Fj be an arbitrary formula of the possible
F's which does occur in some disjunct in
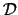
.
There must be
some disjunct in
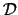
where both
Fj and
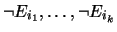
hold.





Next: Eliminating deficiencies: the complete
Up: The construction
Previous: Problems
Joost Joosten
2000-02-07
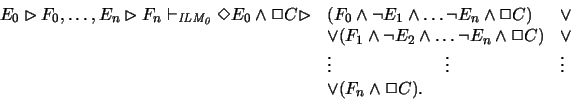
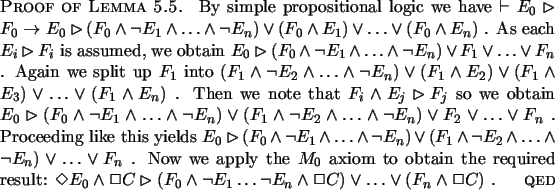
![]() ,
one proceeds as
follows. First a list is made of all relevant sentences of the form
,
one proceeds as
follows. First a list is made of all relevant sentences of the form ![]() .
Let this list be
.
Let this list be
![]() .
You can consider these as the possible deficiencies.
Let x' be such that
x R x' R y and
.
You can consider these as the possible deficiencies.
Let x' be such that
x R x' R y and
![]() .
All deficiencies in x w.r.t. y will be eliminated in such a way
that no new deficiencies will occur in x w.r.t. the newly created
worlds. Again this process shall henceforth be referred to as the
process of making an Sxy-block. The
.
All deficiencies in x w.r.t. y will be eliminated in such a way
that no new deficiencies will occur in x w.r.t. the newly created
worlds. Again this process shall henceforth be referred to as the
process of making an Sxy-block. The ![]() -inclusion of x' shall
be taken into account while creating this Sxy-block.
-inclusion of x' shall
be taken into account while creating this Sxy-block.
![]() .
Let
.
Let ![]() be a permutation of
be a permutation of
![]() .
With any
.
With any ![]() a series of sets
a series of sets
![]() is defined.
is defined.
![]()
![]() .
The notation
.
The notation
![]() stands for the sentence
stands for the sentence
![]() .
With this terminology one can easily
write down the n! useful variants of lemma 5.5.
.
With this terminology one can easily
write down the n! useful variants of lemma 5.5.
![]() lemma 5.3 can be applied. Recall our situation,
x ReB x' R y with
lemma 5.3 can be applied. Recall our situation,
x ReB x' R y with
![]() the
possible deficiencies in x w.r.t. y. So applying lemma 5.3
to any
the
possible deficiencies in x w.r.t. y. So applying lemma 5.3
to any ![]() gives a maximal
gives a maximal
![]() -consistent set containing
one of the disjuncts of the consequent of
-consistent set containing
one of the disjuncts of the consequent of ![]() .
Note that
.
Note that
![]() because
because
![]() .
We now form a set of disjuncts
.
We now form a set of disjuncts
![]() as follows. For every
as follows. For every ![]() you choose the leftmost
disjunct of the consequent which is realizable by
applying lemmas 5.3 and 5.5.
you choose the leftmost
disjunct of the consequent which is realizable by
applying lemmas 5.3 and 5.5.
