



Next: Problems
Up: The modal completeness of
Previous: Tools
The main body of the construction procedure for obtaining our required
 -model is quite analogous to the case of
-model is quite analogous to the case of
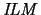 .
One difference is that we now deal with copies of maximal
.
One difference is that we now deal with copies of maximal
 -consistent sets, and that we have to satisfy another frame
condition. The nomenclature will thus be exactly the same. In the
case of
-consistent sets, and that we have to satisfy another frame
condition. The nomenclature will thus be exactly the same. In the
case of
 we will not have ``there are no deficiencies'' as an
invariant. We start again
with an
we will not have ``there are no deficiencies'' as an
invariant. We start again
with an
 -consistent set m0 containing
-consistent set m0 containing
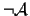 .
If
.
If
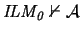 .
Again the only entity that can be defined
globally is the forcing relation
.
Again the only entity that can be defined
globally is the forcing relation 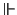 .
We set
.
We set
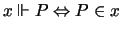 ,
for the propositional variables. The body of the
procedure will now be as follows:
,
for the propositional variables. The body of the
procedure will now be as follows:
-
As a first approximation of the required model, set its domain to be
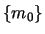 and
and
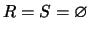 .
.
begin
As long as problems or deficiencies still do exist in the model, enter this
loop:
-
If a problem does exist, then pick one of lowest order and
eliminate this very problem. After having done so, close off under the
frame conditions.
-
If some deficiency exist somewhere, then fix an x and a y, such that
deficiencies in x w.r.t. y do exist. Eliminate all these deficiencies
and close off under the frame conditions.
end
We choose the way of eliminating problems, respectively deficiencies,
cleverly so as to have some useful properties in the model. The useful
properties that we need in our model are stated again as invariants as
they hold at the beginning and at the end of each loop.
- 1.
- The frame is an
 -frame.
-frame.
- 2.
-
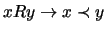 .
.
- 3.
-
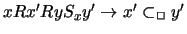 .
.
- 4.
-
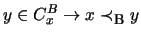 .
.
- 5.
-
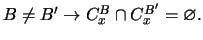
- 6.
-
![$ x R y R z \rightarrow [ \exists \ y' \ x R y' R z \wedge \forall y''
(x R y'' R z \rightarrow y'' \subset_{\Box} y' )] $](img310.gif) .
.
Again one should run through the whole construction checking that these are
indeed invariants. Surely they hold at the beginning of the loop. So we have
to make sure that after every execution of the loop all the invariants hold.




Next: Problems
Up: The modal completeness of
Previous: Tools
Joost Joosten
2000-02-07