



Next: Correctness.
Up: Deficiencies
Previous: Eliminating deficiencies: the complete
All the above ingredients make sure that the logic is complete.
However there is no ingredient that would yield the finiteness of the
model. In proving the completeness of
 an infinite model is
thus provided as the limit of an iterative process. In the limit
neither problems nor deficiencies should be present. Most likely,
eliminating a problem or a deficiency will create many new problems
and deficiencies as a side effect. It should be made sure that every
problem or deficiency is at some stage eliminated. This can be done by
adequate labeling as is also done in [MVar]. By means of a
set I, the set of imperfections we will keep track of all the
problems and deficiencies which have not yet been eliminated. The
model construction can thus be represented by the following procedure.
an infinite model is
thus provided as the limit of an iterative process. In the limit
neither problems nor deficiencies should be present. Most likely,
eliminating a problem or a deficiency will create many new problems
and deficiencies as a side effect. It should be made sure that every
problem or deficiency is at some stage eliminated. This can be done by
adequate labeling as is also done in [MVar]. By means of a
set I, the set of imperfections we will keep track of all the
problems and deficiencies which have not yet been eliminated. The
model construction can thus be represented by the following procedure.
-
The first approach to the model will be to take the domain
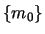 and
and
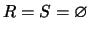 .
All the problems of m0 are stored in I.
.
All the problems of m0 are stored in I.
As long as I is nonempty repeat the following actions.
-
Select the oldest member of I. If this is not uniquely defined, just
pick arbitrarily one of the oldest. Old refers of course to how many
repetitions the element has already been in I.
-
If this oldest member of I is a problem
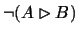 in some
world x, eliminate it by defining xReBy for an adequate
y. This y is provided by lemma 5.2 and as usual is
chosen such that
in some
world x, eliminate it by defining xReBy for an adequate
y. This y is provided by lemma 5.2 and as usual is
chosen such that
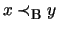 and
and 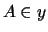 .
.
-
If the oldest member of I is a deficiency in some world x w.r.t. some world y, then eliminate it by making an Sxy-block.
-
Close off under the
 frame conditions in a minimal way. Add the
new freshly born problems and deficiencies to I.
frame conditions in a minimal way. Add the
new freshly born problems and deficiencies to I.
This construction method produces a whole series of
 -models
-models
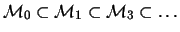 .
With each execution of the repeat loop the previous model is
extended. In general, for no
.
With each execution of the repeat loop the previous model is
extended. In general, for no
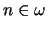 ,
,
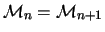 will hold. But one can consider
will hold. But one can consider
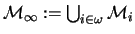 .
It is clear that in
.
It is clear that in
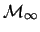 neither problems nor deficiencies hold. This of course under the
assumption that all the invariants we used throughout the construction
are indeed invariants, and also hold for the infinite model. If this
is true, then problems that have been eliminated will never
re-emerge. This is reflected by invariant 4. The main strategy
for proving the invariants will be to prove their correctness for all
neither problems nor deficiencies hold. This of course under the
assumption that all the invariants we used throughout the construction
are indeed invariants, and also hold for the infinite model. If this
is true, then problems that have been eliminated will never
re-emerge. This is reflected by invariant 4. The main strategy
for proving the invariants will be to prove their correctness for all
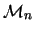 ,
and then show that this extends to the infinite
model. Before doing so it is useful to note some features of the chain
of models
,
and then show that this extends to the infinite
model. Before doing so it is useful to note some features of the chain
of models
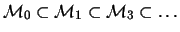 .
First of all one can say there is a uniform upper bound to the height
of the model. (The height is defined as the maximal length of some
chain
.
First of all one can say there is a uniform upper bound to the height
of the model. (The height is defined as the maximal length of some
chain
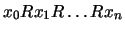 in the model.) Therefore
in the model.) Therefore
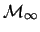 also has finite height. Thus
also has finite height. Thus
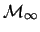 is conversely well-founded
when it comes to the R-relation. Second and also important, one can
see that
is conversely well-founded
when it comes to the R-relation. Second and also important, one can
see that
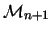 is sort of an ``end extension'' of
is sort of an ``end extension'' of
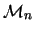 in the sense that no intermediate worlds will be added. So, if
in the sense that no intermediate worlds will be added. So, if
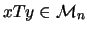 and
and
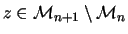 ,
then for no z, xTzTy for both T=Sxi as well as for
T=R. Further it is clear that all defined notions like
,
then for no z, xTzTy for both T=Sxi as well as for
T=R. Further it is clear that all defined notions like
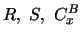 ,
etc. are weakly monotonic increasing entities.
,
etc. are weakly monotonic increasing entities.




Next: Correctness.
Up: Deficiencies
Previous: Eliminating deficiencies: the complete
Joost Joosten
2000-02-07
![]() -models
-models
![]() .
With each execution of the repeat loop the previous model is
extended. In general, for no
.
With each execution of the repeat loop the previous model is
extended. In general, for no
![]() ,
,
![]() will hold. But one can consider
will hold. But one can consider
![]() .
It is clear that in
.
It is clear that in
![]() neither problems nor deficiencies hold. This of course under the
assumption that all the invariants we used throughout the construction
are indeed invariants, and also hold for the infinite model. If this
is true, then problems that have been eliminated will never
re-emerge. This is reflected by invariant 4. The main strategy
for proving the invariants will be to prove their correctness for all
neither problems nor deficiencies hold. This of course under the
assumption that all the invariants we used throughout the construction
are indeed invariants, and also hold for the infinite model. If this
is true, then problems that have been eliminated will never
re-emerge. This is reflected by invariant 4. The main strategy
for proving the invariants will be to prove their correctness for all
![]() ,
and then show that this extends to the infinite
model. Before doing so it is useful to note some features of the chain
of models
,
and then show that this extends to the infinite
model. Before doing so it is useful to note some features of the chain
of models
![]() .
First of all one can say there is a uniform upper bound to the height
of the model. (The height is defined as the maximal length of some
chain
.
First of all one can say there is a uniform upper bound to the height
of the model. (The height is defined as the maximal length of some
chain
![]() in the model.) Therefore
in the model.) Therefore
![]() also has finite height. Thus
also has finite height. Thus
![]() is conversely well-founded
when it comes to the R-relation. Second and also important, one can
see that
is conversely well-founded
when it comes to the R-relation. Second and also important, one can
see that
![]() is sort of an ``end extension'' of
is sort of an ``end extension'' of
![]() in the sense that no intermediate worlds will be added. So, if
in the sense that no intermediate worlds will be added. So, if
![]() and
and
![]() ,
then for no z, xTzTy for both T=Sxi as well as for
T=R. Further it is clear that all defined notions like
,
then for no z, xTzTy for both T=Sxi as well as for
T=R. Further it is clear that all defined notions like
![]() ,
etc. are weakly monotonic increasing entities.
,
etc. are weakly monotonic increasing entities.