



Next: The construction
Up: The modal completeness of
Previous: General outline of the
Definition 5.1
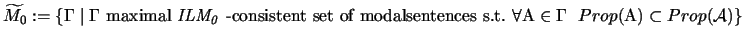
.
Prop(
B) is the set of propositional
variables
occurring in
B.
The definitions of 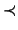 and
and
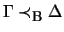 are precisely
as before.
are precisely
as before.
In perfect analogy with the case of
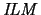 we have the following
two lemmas:
we have the following
two lemmas:
Lemma 5.2
Let
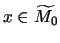
and
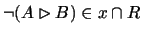
.
There exists
y such that
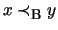
and
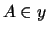
.
Moreover,
y can be chosen to contain a
``maximal amount'' of

-formulas.
The M0-axiom is essentially used only in the next
lemma.
Lemma 5.4
Consider
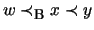
,
all in
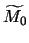
,
such that
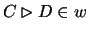
,
and
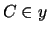
.
Then there exists
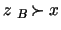
with both
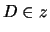
and
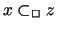
.
This
z can be chosen to
be maximal w.r.t. the

-inclusion.
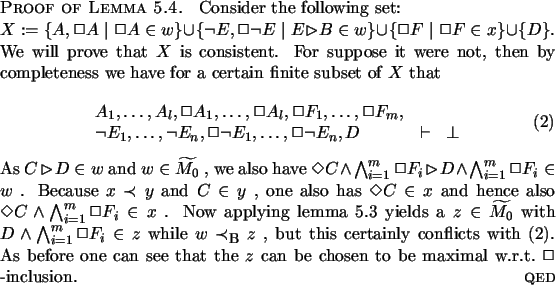
Joost Joosten
2000-02-07
![]() and
and
![]() are precisely
as before.
are precisely
as before.
![]() we have the following
two lemmas:
we have the following
two lemmas:![]() with
with
![]() and let
and let
![]() be such that
be such that
![]() and
and
![]() .
There exists
.
There exists
![]() , with
, with ![]() .
.