



Next: Tools
Up: The modal completeness of
Previous: The modal completeness of
By the same means by which the modal completeness of
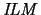 was verified, we now obtain a new result: the modal completeness of
was verified, we now obtain a new result: the modal completeness of
 .
Again a countermodel is built by successively
eliminating problems and deficiencies. Since in this case we have not
succeeded in proving the finite model property we will not strive for
termination of the construction. In the new case we have to end up
with an
.
Again a countermodel is built by successively
eliminating problems and deficiencies. Since in this case we have not
succeeded in proving the finite model property we will not strive for
termination of the construction. In the new case we have to end up
with an
 -frame. Let us recall the
-frame. Let us recall the
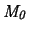 -axiom
and its corresponding frame condition. M0 is the axiom
-axiom
and its corresponding frame condition. M0 is the axiom
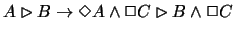 and its frame condition is:
and its frame condition is:
In order to obtain this property in our model consisting of copies of
maximal
 -consistent sets of modal sentences, it
suffices to choose y such that
-consistent sets of modal sentences, it
suffices to choose y such that
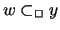 .
It turns out to
be possible to do so. Fix again an
.
It turns out to
be possible to do so. Fix again an
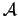 such that
such that
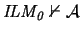 .
(Again this font is a little
unusual in the modal setting, but we again want to have the A free
to use in the course of this chapter.) The set of relevant formulas
R is as before, the smallest set of formulas containing
.
(Again this font is a little
unusual in the modal setting, but we again want to have the A free
to use in the course of this chapter.) The set of relevant formulas
R is as before, the smallest set of formulas containing
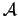 and closed under taking subformulas and single
negations. As
and closed under taking subformulas and single
negations. As
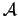 is not derivable in
is not derivable in
 there exists a maximal
there exists a maximal
 -consistent set m0containing
-consistent set m0containing
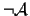 .
A model
.
A model
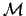 is built above this m0 so
that the truth lemma will hold for all relevant formulas, and thus
is built above this m0 so
that the truth lemma will hold for all relevant formulas, and thus
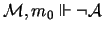 .
We have to provide ourselves with some tools
before we can start with the actual construction.
.
We have to provide ourselves with some tools
before we can start with the actual construction.




Next: Tools
Up: The modal completeness of
Previous: The modal completeness of
Joost Joosten
2000-02-07