



Next: The modal completeness of
Up: Correctness and termination
Previous: Correctness and termination
By proving the correctness of the invariants we have also justified the
claims based on them. It remains to show that the construction is overall
correct. Indeed problems and deficiencies are eliminated successively, but
is this sufficient? Once a deficiency in x w.r.t. y is eliminated, it is
clear that it will never turn up again. Every new stage of the model is
properly extending the previous one. So y Sx y', once there, will never
disappear. A problem
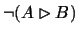 in x is eliminated by creating
a B-critical successor y where A holds. Invariant 3 implies
that
in x is eliminated by creating
a B-critical successor y where A holds. Invariant 3 implies
that
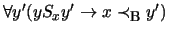 .
This means that
at every new stage of the model no problems that have already been dealt with
will reoccur.
.
This means that
at every new stage of the model no problems that have already been dealt with
will reoccur.
The construction can be seen as repeatedly eliminating a problem and
then all the new deficiencies that emerge by tackling the problem. It
should be noted that, during all of this process, the new worlds that
are added are of higher order then the order of the world in which the
problem occurred. This gives an inductive flavor. And indeed one can
show that the order has an upper bound. For if
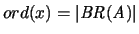 ,
one has
,
one has
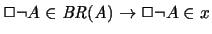 .
But as
.
But as
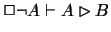 ,
also
,
also
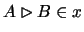 .
This also holds for all relevant formulas, so no
problems will exist once
.
This also holds for all relevant formulas, so no
problems will exist once
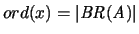 .
In the model every non-circular path (using R and S transitions) will
finally end up in such a top node. So the processs will indeed stop.
(In other words, the strictly monotonic increase of the order function
together with the upper bound on the function enforces the termination of the
process.)
.
In the model every non-circular path (using R and S transitions) will
finally end up in such a top node. So the processs will indeed stop.
(In other words, the strictly monotonic increase of the order function
together with the upper bound on the function enforces the termination of the
process.)




Next: The modal completeness of
Up: Correctness and termination
Previous: Correctness and termination
Joost Joosten
2000-02-07