



Next: The other principles
Up: The landscape: Interpretability
Previous: The formalization of interpretability
Valid arithmetical principles
Some principles are easily seen to hold in a general arithmetical
setting. From now on we will only study arithmetical theories that are
reasonable. As mentioned before, reasonable can be read as
``containing
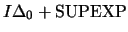 ''. We will treat some
principles which hold in every reasonable arithmetical
theory. Precisely these principles are later collected to be studied
in a modal setting.
''. We will treat some
principles which hold in every reasonable arithmetical
theory. Precisely these principles are later collected to be studied
in a modal setting.
-
We call J1 the principle of
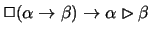 .
This reflects the fact that the
identity function is a special case of an interpretation. If one takes
J in (+) to be the identity, a tautology arises. (The relativizing
formula can in this example just be taken x=x.)
.
This reflects the fact that the
identity function is a special case of an interpretation. If one takes
J in (+) to be the identity, a tautology arises. (The relativizing
formula can in this example just be taken x=x.)
-
The principle J2 reads
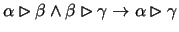 .
We already encountered a plea for
this principle when we viewed it as a statement of models. By more
elementary means one can also see this principle to be true. The
observation that the composition of two interpretations is again an
interpretation, more or less explains the principle. Finally one
should convince oneself that this reasoning can be done within the
theory. (Here one has to use technical facts like
.
We already encountered a plea for
this principle when we viewed it as a statement of models. By more
elementary means one can also see this principle to be true. The
observation that the composition of two interpretations is again an
interpretation, more or less explains the principle. Finally one
should convince oneself that this reasoning can be done within the
theory. (Here one has to use technical facts like
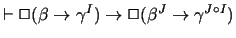 .)
.)
-
The principle J3 is
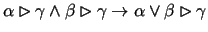 .
Reading this as a
statement of models legitimizes it immediately. If in any model of A,
and in any model of B, one can define a submodel for C, well then
in any model of
.
Reading this as a
statement of models legitimizes it immediately. If in any model of A,
and in any model of B, one can define a submodel for C, well then
in any model of 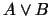 one can define a submodel for C. For if
one can define a submodel for C. For if
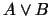 holds, either one of them holds, but in both cases a model
of C can be defined. In terms of interpretations J3 reflects that
one can choose which interpretation to use, depending on
holds, either one of them holds, but in both cases a model
of C can be defined. In terms of interpretations J3 reflects that
one can choose which interpretation to use, depending on 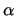 or
or
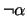 to hold.
to hold.
-
Another principle, J4:
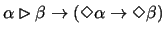 ,
reflects that interpretations
yield relative consistency results. One can also see J4 to be a
direct consequence of J1 and J2. For this we write the consequent
as
,
reflects that interpretations
yield relative consistency results. One can also see J4 to be a
direct consequence of J1 and J2. For this we write the consequent
as
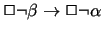 .
Now suppose
.
Now suppose
 and
and
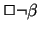 .
J1 gives that
.
J1 gives that
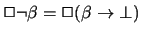 implies
implies
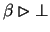 .
By transitivity
, (J2), one gets
.
By transitivity
, (J2), one gets
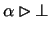 .
But as the translation of
.
But as the translation of 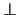 under any interpretation is always
under any interpretation is always 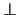 ,
we automatically get
,
we automatically get
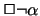 .
.
-
The principle J5 reads
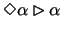 .
It can be seen
as an arithmetized version of the completeness theorem. The
consistency of a statement implies the existence of a model on which
this statement holds. As the theories we consider are strong enough to
encode the whole Henkin construction, one can prove within that very
theory
.
It can be seen
as an arithmetized version of the completeness theorem. The
consistency of a statement implies the existence of a model on which
this statement holds. As the theories we consider are strong enough to
encode the whole Henkin construction, one can prove within that very
theory
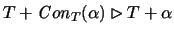 .
This coding can be
done in a really weak theory,
.
This coding can be
done in a really weak theory,
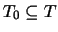 ,
so actually something
stronger can be proven as well:
,
so actually something
stronger can be proven as well:
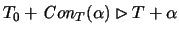 .
This strengthening of J5 is essentially used in
establishing the arithmetical validity of the new principle P0 in
paragraph 6.5.
.
This strengthening of J5 is essentially used in
establishing the arithmetical validity of the new principle P0 in
paragraph 6.5.
All these principles are collected together in a modal logic. This
modal logic is properly defined in chapter 3. It will be
referred to as
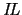 .
.




Next: The other principles
Up: The landscape: Interpretability
Previous: The formalization of interpretability
Joost Joosten
2000-02-07
![]() .
.