



Next: The modal logic of
Up: The landscape: Interpretability
Previous: Valid arithmetical principles
The other principles
If the theory under consideration is
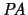 with full
induction, more principles hold. We consider Montagna's principle
with full
induction, more principles hold. We consider Montagna's principle
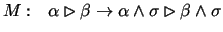 for
every
for
every
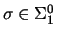 .
This can be seen to hold for
.
This can be seen to hold for
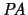 using the following fact. Over
using the following fact. Over
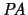 one knows that
one knows that
 iff every
iff every
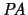 -model of
-model of 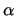 has an end extension which is
a
has an end extension which is
a
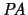 -model of
-model of 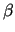 .
So if the
.
So if the
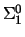 -sentence
-sentence 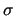 holds in a
holds in a
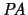 -model M of
-model M of 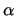 ,
there must be a witness in
this model for
,
there must be a witness in
this model for 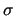 .
This witness serves as a witness as well in
any end extension of M. We say that
.
This witness serves as a witness as well in
any end extension of M. We say that 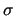 is being preserved
under taking end extensions. So there exists an end extension for
is being preserved
under taking end extensions. So there exists an end extension for
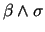 ,
hence
,
hence
 .
.
If T, the theory under consideration, is finitely axiomatizable, the
situation gets a lot easier. The sentence
 can just be
replaced by
can just be
replaced by
 ,
where
,
where  is the
conjunction of all the axioms of T. Consequently the sentence (+),
expressing formal interpretability, becomes a
is the
conjunction of all the axioms of T. Consequently the sentence (+),
expressing formal interpretability, becomes a
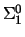 -sentence
and hence can be ``boxed up'', using so-called provable
-sentence
and hence can be ``boxed up'', using so-called provable
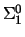 -completeness already used by Gödel. By doing so one
obtains the so-called persistence principle
-completeness already used by Gödel. By doing so one
obtains the so-called persistence principle
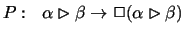 .
As
.
As 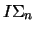 is finitely axiomatizable
for all
is finitely axiomatizable
for all
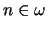 ,
we have that P is an interpretability
principle for
,
we have that P is an interpretability
principle for 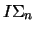 for all
for all
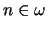 .
.




Next: The modal logic of
Up: The landscape: Interpretability
Previous: Valid arithmetical principles
Joost Joosten
2000-02-07
![]() can just be
replaced by
can just be
replaced by
![]() ,
where
,
where ![]() is the
conjunction of all the axioms of T. Consequently the sentence (+),
expressing formal interpretability, becomes a
is the
conjunction of all the axioms of T. Consequently the sentence (+),
expressing formal interpretability, becomes a
![]() -sentence
and hence can be ``boxed up'', using so-called provable
-sentence
and hence can be ``boxed up'', using so-called provable
![]() -completeness already used by Gödel. By doing so one
obtains the so-called persistence principle
-completeness already used by Gödel. By doing so one
obtains the so-called persistence principle
![]() .
As
.
As ![]() is finitely axiomatizable
for all
is finitely axiomatizable
for all
![]() ,
we have that P is an interpretability
principle for
,
we have that P is an interpretability
principle for ![]() for all
for all
![]() .
.