



Next: Concluding
Up: A new principle
Previous: A relation between M
The arithmetical validity of P0
The new principle P0 is next seen to be arithmetically valid. The
argument is due to Albert Visser and can be presented in five basic
steps. We will use here standard notation and well-known facts of
arithmetization. For a good background one can consult very clear
texts like for example [Vis90], [JdJ98]. In the
sequel of this paragraph  and
and 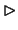 will stand again for
formalized provability and interpretability respectively. These
notions are dependent on the base theory in which they are
formalized. In case of possible confusion we will write this base
theory by indexing the operator, e.g.
will stand again for
formalized provability and interpretability respectively. These
notions are dependent on the base theory in which they are
formalized. In case of possible confusion we will write this base
theory by indexing the operator, e.g. 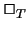 .
We have to prove that
in any reasonable arithmetical theory
.
We have to prove that
in any reasonable arithmetical theory
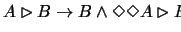 is derivable.
is derivable.
For any reasonable arithmetical theory T:
- 1.
- Suppose
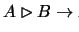 and reason within the theory. We thus
have
and reason within the theory. We thus
have
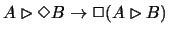 .
.
- 2.
- We can now take a finite subtheory T0 of T which is sufficiently
strong. We will not be too precise about this. The actual constraints
on T0 can be distilled from the following argument. It seems
natural to demand that T0 can code the Henkin construction used in
the completeness theorem. By this one can obtain a stronger variant of
J5 as is outlined later on. We have
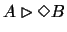 ,
which turns out to be a
,
which turns out to be a
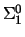 -sentence as T0 is a finite
theory. The
-sentence as T0 is a finite
theory. The 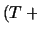 -sentence (modulo notational inaccuracies)
-sentence (modulo notational inaccuracies)
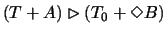 can be replaced by the
can be replaced by the
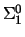 -sentence
-sentence
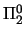 ,
where J is the
interpretation used in 1 an
,
where J is the
interpretation used in 1 an 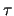 is the conjunction of all
the axioms of T0.
is the conjunction of all
the axioms of T0.
- 3.
- We can thus conclude
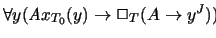 .
This
follows from 2 and the provable
.
This
follows from 2 and the provable
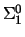 -completeness of
T.
-completeness of
T.
- 4.
- The axiom
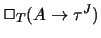 reflects the
completeness theorem. As the whole Henkin construction can be coded
within T, in T one can prove
reflects the
completeness theorem. As the whole Henkin construction can be coded
within T, in T one can prove
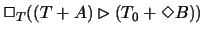 .
But
actually something stronger holds as well. The finite theory T0 is
chosen strong enough to perform the Henkin construction for T. So
within T one can prove
.
But
actually something stronger holds as well. The finite theory T0 is
chosen strong enough to perform the Henkin construction for T. So
within T one can prove
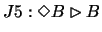 .
With
necessitation one obtains
.
With
necessitation one obtains
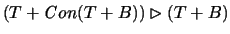 .
.
- 5.
- The final step consists of combining 3 and 4. The
transitivity of
 under the
under the  yields the desired result,
that is
yields the desired result,
that is
 .
.




Next: Concluding
Up: A new principle
Previous: A relation between M
Joost Joosten
2000-02-07
![]() and
and ![]() will stand again for
formalized provability and interpretability respectively. These
notions are dependent on the base theory in which they are
formalized. In case of possible confusion we will write this base
theory by indexing the operator, e.g.
will stand again for
formalized provability and interpretability respectively. These
notions are dependent on the base theory in which they are
formalized. In case of possible confusion we will write this base
theory by indexing the operator, e.g. ![]() .
We have to prove that
in any reasonable arithmetical theory
.
We have to prove that
in any reasonable arithmetical theory
![]() is derivable.
is derivable.