The basic interpretability logic

The language of the modal interpretability logic is the language of provability logic extended with a binary modality $\rhd$. So we have at our disposal an enumerable supply of propositional variables, a unary modality $\Box$ and a binary modality $\rhd$. We can either use all the Boolean connectives or just constrain ourselves to $\wedge$and $\neg$. We adhere to some reading conventions as to omit parentheses without introducing ambiguities. The negation, the diamond and the box bind stronger than $\wedge$ and $\vee$, which in turn bind stronger then $\rhd$ and $\rightarrow$. Finally we say that $\rhd$binds stronger than $\rightarrow$. So $A\rhd B\rightarrow A\wedge \Box C\rhd B\wedge \Box C$, for example, is short for $(A\rhd B)\rightarrow ((A\wedge (\Box C)\rhd (B\wedge (\Box C))))$.

Definition 3.1   The basic interpretability logic $\mathit{IL}$ has the following axiom schemes:

$$\begin{array}{l} L_1 :\ \ \ \Box (A\rightarrow B)\rightarrow ... ...ghtarrow \Diamond B) \\ J5 :\ \ \ \Diamond A\rhd A \end{array}$$

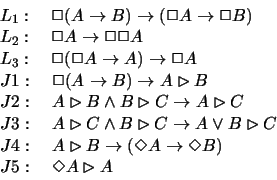
The rules of inference are modus ponens and necessitation, that is, if one has $\vdash A\rightarrow B$ and $\vdash A$, then also $\ \vdash B$, resp. $\vdash A\Rightarrow \ \vdash \Box A$.

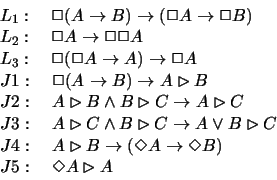
Just as with provability logic, a Kripke-like semantics is given for $\mathit{IL}$.

Definition 3.2   An $\mathit{IL}$-frame (also Veltman-frame) is a triple
$( W,R,\{ S_w\mid w\in W\} )$ such that:

1.

(W,R) is an L-frame, that is, W is a non empty set and R is a transitive conversely well-founded relation on W².

2.

  $S_w\subset w\uparrow \times w\uparrow$ $(w\uparrow := \{x \in W \mid wRx \} )$.

3.

  $(R\cap w\uparrow )\subset S_w$.

4.

 S_w is reflexive.

5.

 S_w is transitive.

By S we mean $\cup \{ S_w\mid w\in W\}$. The elements of W will also be called worlds or nodes.

Definition 3.3   An $\mathit{IL}$-model is an $\mathit{IL}$-frame together with a forcing relation $\Vdash$ between worlds and propositional letters. $\Vdash$ is extended to formulas by defining $\Vdash$ to commute with the Boolean connectives and defining

-

$w\Vdash \Box A\Leftrightarrow \forall w' (wRw'\rightarrow w'\Vdash A)$,

-

$w\Vdash A\rhd B\Leftrightarrow \forall w'(wRw'\wedge w'\Vdash A\rightarrow \exists w''(w'S_ww''\wedge w''\Vdash B))$.

One could also first define $\Vdash$ and later determine the conditions on the binary relations S_w. In this manner one notices some frame correspondences. We see that J4 imposes 2, J1corresponds with 4, J2 corresponds with 5 and J5 corresponds with 3. The axiom J3 has a special status as it does not impose anything on the frames.

Definition 3.4  

• $M,w\Vdash A$ and $w\Vdash A$ are equivalent expressions.
• $M\models A$ means that for all w in M, $M,w\Vdash A$.
• If F is a Veltman-frame, $F\models A$ means that for any $\Vdash$, $(F,\Vdash )\models A$.
• We say that A holds as a scheme on a frame F if all instantiations of A hold at F.
• Let $\mathcal{K}$ be a class of Veltman-frames. We define $\mathcal{K}\models A$ iff
  $\forall F\in \mathcal{K}\ F\models A$.

As every axiom of $\mathit{IL}$ is valid on every Veltman-frame, and this validity is preserved under the rules of inference, we see that $\mathit{IL}$is sound w.r.t. Veltman-frames. That is, all $\mathit{IL}$-derivable formulas hold on all Veltman-frames. The logic is modally complete as well. See [JV91]. So if a formula holds on all $\mathit{IL}$-frames, it must be derivable in $\mathit{IL}$. This completeness result is also presented for example in [JdJ98].

Throughout this paper we will use some very basic results of $\mathit{IL}$. Most of them are very easy to verify. In the next lemma we expose some facts of $\mathit{IL}$.

Lemma 3.5  

-

$\mathit{IL}\vdash A\rhd \bot \leftrightarrow \Box \neg A$

-

$\mathit{IL}\vdash \Box \neg A \rightarrow A\rhd B$

-

$\mathit{IL}\vdash A\vee \Diamond A\rhd A$

-

$\mathit{IL}\vdash A\rhd A\wedge \Box \neg A$

These facts are indeed easy to verify as is partly done in [JdJ98]. Formal proofs in $\mathit{IL}$ are quite laborious to write down. A Gentzen proof system is most likely hard to find.