More principles and frame correspondences

Other axioms we will consider are:

$$\begin{array}{ll} P &:\ \ \ A\rhd B\rightarrow \Box (A\rhd B)... ...&:\ \ \ A\rhd \Diamond B\rightarrow \Box (A\rhd B) \end{array}$$

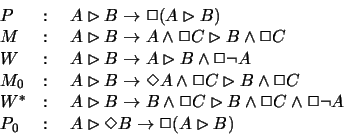
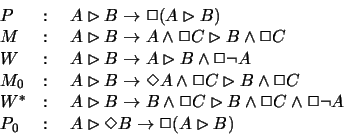
Definition 3.6   The logic ${\mathit ILX}$ is a modal logic in the language $\Box$, $\rhd$. All tautologies in this language are theorems of ${\mathit ILX}$. Further are all the axiom schemes of $\mathit{IL}$ plus X itself, axiom schemes of ${\mathit ILX}$. The rules of inference are modus ponens and the rule of necessitation. X can be taken to be one of the above axiom schemes. The logic ILXY is the logic where we add both X and Y as axiom schemes.

The logic $\mathit{ILW}^*$ is known to be precisely $\mathit{ILM_0}W$. See for example [Vis97]. All the logics we will consider over $\mathit{IL}$, will have the deduction theorem. The principle P₀ is introduced here for the first time. The principles P, M, etc., do not hold on every $\mathit{IL}$-frame. One can examine which condition the frame should satisfy in order to have the principle to hold. We obtain the following list of frame correspondences:

$$\begin{array}{ll} P&:\ \ \ xRx'Ry\wedge yS_xy'\rightarrow yS_... ... P_0&:\ \ \ xRx'Rx''S_xyRy'\rightarrow x''S_{x'}y'. \end{array}$$

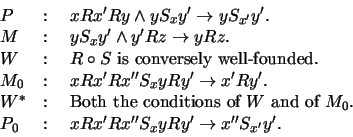
Instead of the formula one could read its universal closure. The frame condition of W is not first-order expressible though. The general problem of first order definability of a frame condition is known to be undecidable even in pure modal logic, and presumably even for extensions of Löbs logic, see Chagrova [Cha91], and is conjectured by van Benthem to be much worse. In [Ben84] he shows that the first-order definability for monadic second-order $\Pi^1_1$ sentences of a restricted form is non-arithmetically definable. The situation with interpretability logic is likely to be at least as complex. In a joint paper, Carlos Areces, Dick de Jongh and Eva Hoogland establish the interpolation property for $\mathit{IL}$, see [AdJH98]. As $\mathit{IL}$ is a ``nice'' logic and as it has interpolation, they show, it must have the Beth property and hence fixed points; so any logic ${\mathit ILX}$ has fixed points and thus, generalizing a result of Maksimova, also the Beth property.