First one could try to descend to theories weaker than
The logic of interpretability can thus be viewed as an extension to
the logic of provability. The logic of provability includes important
results concerning formal provability and provides a very
sophisticated way of representing important results of, for example,
Gödel, [Göd92], and Löb, [Löb55]. The
subject of study in provability logic as with interpretability logic
is formal theories. Provability is quite a stable notion though and
does not distinguish between even very different theories. From quite
weak theories onwards, all the provability logics come out the
same. It is known that all theories in which
![]() is interpretable and which are
is interpretable and which are ![]() -sound under
the translation, have the same provability logic: Löb's logic. See
for example [Vis97], or [Vis84]. One could think
of three approaches if one wants to obtain different logics, for fine
tuning so to say.
-sound under
the translation, have the same provability logic: Löb's logic. See
for example [Vis97], or [Vis84]. One could think
of three approaches if one wants to obtain different logics, for fine
tuning so to say.
First one could try to descend to theories weaker than
![]() ,
where Löbs logic is still arithmetically valid. This
becomes an extremely difficult venture and despite intensive
investigations very little is known on this subject. See e.g. [BV93]. Another direction would be to alter the bare logic.
One could switch to, for example, intuitionistic logic in its relation
to Heyting arithmetic obtaining a variety of new valid
principles. Significant progress is made, [Iem98],
[Vis94], but for example it is still unknown whether the
provability logic of Heyting Arithmetic is axiomatizable at all. A
third possibility would be to enrich the modal language. Where the
logic of provability employs only one modal operator
,
where Löbs logic is still arithmetically valid. This
becomes an extremely difficult venture and despite intensive
investigations very little is known on this subject. See e.g. [BV93]. Another direction would be to alter the bare logic.
One could switch to, for example, intuitionistic logic in its relation
to Heyting arithmetic obtaining a variety of new valid
principles. Significant progress is made, [Iem98],
[Vis94], but for example it is still unknown whether the
provability logic of Heyting Arithmetic is axiomatizable at all. A
third possibility would be to enrich the modal language. Where the
logic of provability employs only one modal operator ![]() ,
for
formal provability, the language of interpretability logic includes
also a binary modality
,
for
formal provability, the language of interpretability logic includes
also a binary modality ![]() for interpretability. Although
for interpretability. Although ![]() can be defined in terms of
can be defined in terms of ![]() ,
one prefers to use both
modalities. The whole provability logic now becomes a sublogic of the
logic of interpretability. Moreover, distinctions between different
theories are reflected by having different corresponding
interpretability logics. So, interpretability is not that stable a
notion as provability is. Furthermore, all sorts of arithmetical
results can now be expressed, as we will see later, very elegantly
like for example the model existence lemma,
,
one prefers to use both
modalities. The whole provability logic now becomes a sublogic of the
logic of interpretability. Moreover, distinctions between different
theories are reflected by having different corresponding
interpretability logics. So, interpretability is not that stable a
notion as provability is. Furthermore, all sorts of arithmetical
results can now be expressed, as we will see later, very elegantly
like for example the model existence lemma,
![]() ,
or a more intricate formalization of the second
incompleteness theorem of Gödel,
,
or a more intricate formalization of the second
incompleteness theorem of Gödel,
![]() .
.
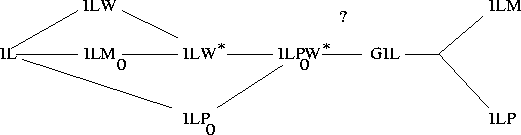
For two main interpretability logics, arithmetical completeness results
are known. On the one hand that is the interpretability logic of
![]() ,
,
![]() ,
and on the other hand the interpretability
logic of any (sufficiently strong) finitely axiomatizable theory,
,
and on the other hand the interpretability
logic of any (sufficiently strong) finitely axiomatizable theory,
![]() .
As these two logics are different, it seems very
natural to ask for the core logic, that is the interpretability logic
of all reasonable arithmetical theories. ``Reasonable'' in this
context is not such a tight notion and can be read here as
``containing
.
As these two logics are different, it seems very
natural to ask for the core logic, that is the interpretability logic
of all reasonable arithmetical theories. ``Reasonable'' in this
context is not such a tight notion and can be read here as
``containing
![]() ''. Looking for this notion is not just a
matter of a simple intersection of all logics; Stronger logics can
prove more but also have more expressive power. The primary aim of
this paper is to contribute to the quest for the interpretability
logic of all reasonable arithmetical theories. In due time many
seemingly relevant interpretability logics have seen the light and many of
them faded away already. The situation at the start of this research
is sketched below.
''. Looking for this notion is not just a
matter of a simple intersection of all logics; Stronger logics can
prove more but also have more expressive power. The primary aim of
this paper is to contribute to the quest for the interpretability
logic of all reasonable arithmetical theories. In due time many
seemingly relevant interpretability logics have seen the light and many of
them faded away already. The situation at the start of this research
is sketched below.
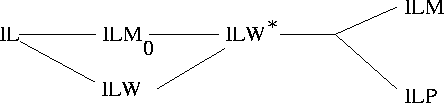
![]() ,
,
![]() and
and
![]() are known to be decidable and
modally complete.
are known to be decidable and
modally complete.
![]() and
and
![]() are also arithmetically
complete with regard to some theories. See e.g. [JdJ98]. In an article soon to appear, [dJV],
are also arithmetically
complete with regard to some theories. See e.g. [JdJ98]. In an article soon to appear, [dJV],
![]() is shown to be decidable and modally complete. In
[Vis90]
is shown to be decidable and modally complete. In
[Vis90]
![]() was put forward as the interpretability
logic of all reasonable arithmetical theories. After the discovery
that M0 is a valid principle in [Vis91], the conjecture
was updated to
was put forward as the interpretability
logic of all reasonable arithmetical theories. After the discovery
that M0 is a valid principle in [Vis91], the conjecture
was updated to
![]() .
.
By the end of this paper we obtain a new picture which is given below.
We develop a strategy for obtaining modal completeness without
necessarily also obtaining decidability. This method is applied to
![]() to get both completeness and decidability. The same method
shows to be fruitful when it is applied to
to get both completeness and decidability. The same method
shows to be fruitful when it is applied to
![]() ;
we obtain the
modal completeness of
;
we obtain the
modal completeness of
![]() .
.
![]() is shown to be inadequate as a
candidate for
is shown to be inadequate as a
candidate for
![]() ,
the logic of all reasonable arithmetical
theories. This is done by introducing a new arithmetically valid
principle P0, which is not derivable over
,
the logic of all reasonable arithmetical
theories. This is done by introducing a new arithmetically valid
principle P0, which is not derivable over
![]() .
.