



Next: The enclosure of
Up: A new principle
Previous: A new principle
When the research to the modal completeness of
 was renewed by
the author, it was suggested that
was renewed by
the author, it was suggested that
 might be modally incomplete.
Certainly this would not be the first modally incomplete
principle. Albert Visser tried to strengthen the frame condition of
might be modally incomplete.
Certainly this would not be the first modally incomplete
principle. Albert Visser tried to strengthen the frame condition of
 to arrive at a stronger principle. The frame condition of
to arrive at a stronger principle. The frame condition of
 is:
is:
Instead of demanding an R-relation between x1 and y', one can
demand an Sx1-relation between x2 and y'. As we have
x2Sx1y', we must also have x1Ry', so indeed the frame
condition is hereby strengthened. The corresponding principle is
readily found and baptized with the lyrical name of P0.
At first M1 was suggested as a name, but at second thought P0seemed to be more appropriate. The reason is given below. As P0turns out to be an arithmetically valid principle one is obliged to subject
it to a modal and comparative analysis. The target logic is the
interpretability logic of all reasonable arithmetical theories,
abbreviated
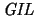 .
As P0 is a new generally valid principle, it
brings us one step closer to
.
As P0 is a new generally valid principle, it
brings us one step closer to
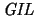 .
.




Next: The enclosure of
Up: A new principle
Previous: A new principle
Joost Joosten
2000-02-07