



Next: Making an SNy-block.
Up: The details of constructing
Previous: The details of constructing
``Making an Sxy-block'' is the process which is applied to eliminate
all deficiencies in x w.r.t. y, when
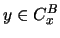 for some B.
Eliminating a deficiency in x w.r.t. y is nothing but providing
an Sx-successor of y that suits the job. If we want to respect
invariant 3 we must ensure that every Sx-successor of
y is B-critical as well. It turns out to be possible to define a finite
construction of Sx-successors of y such that no deficiency remains in
x w.r.t. y and w.r.t. the whole Sxy-block, and such that moreover
this whole construction lies B-critically above x. This is our so-called
process of ``making an Sxy-block'', and it proceeds as follows.
for some B.
Eliminating a deficiency in x w.r.t. y is nothing but providing
an Sx-successor of y that suits the job. If we want to respect
invariant 3 we must ensure that every Sx-successor of
y is B-critical as well. It turns out to be possible to define a finite
construction of Sx-successors of y such that no deficiency remains in
x w.r.t. y and w.r.t. the whole Sxy-block, and such that moreover
this whole construction lies B-critically above x. This is our so-called
process of ``making an Sxy-block'', and it proceeds as follows.
Repeat the following steps as long as deficiencies of x w.r.t. the
Sxy-block still do exist.
It is evident that the process of making an Sxy-block will
terminate. There is only a finite number of possible deficiencies of
x w.r.t. any specific y'. This implies that every world in the
Sxy-block needs only a finite number of Sx-successors. An
arbitrary chain (without loops) of Sy-successors is limited in
length due to the maximality of all worlds w.r.t. the
 -inclusion. By the clause ``If there is a y'' in the
Sxy-block with
-inclusion. By the clause ``If there is a y'' in the
Sxy-block with 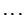 ,
we are forced to use the same y'' again
if it is approppiate. These two ingredients ensure the finiteness of
the Sxy-block.
,
we are forced to use the same y'' again
if it is approppiate. These two ingredients ensure the finiteness of
the Sxy-block.




Next: Making an SNy-block.
Up: The details of constructing
Previous: The details of constructing
Joost Joosten
2000-02-07
![]() -inclusion. By the clause ``If there is a y'' in the
Sxy-block with
-inclusion. By the clause ``If there is a y'' in the
Sxy-block with ![]() ,
we are forced to use the same y'' again
if it is approppiate. These two ingredients ensure the finiteness of
the Sxy-block.
,
we are forced to use the same y'' again
if it is approppiate. These two ingredients ensure the finiteness of
the Sxy-block.