



Next: Correctness and termination
Up: The details of constructing
Previous: Making an Sxy-block.
The procedure of ``making an SNy-block'' is quite similar to that
of ``making an Sxy-block''. The main difference is that we are
eliminating deficiencies here of a whole bunch of worlds at the same
time. Another thing is that we are not too worried about criticalness.
Of all the worlds in N, for at most one 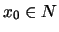 ,
we have that
,
we have that
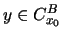 by invariant 5. The procedure of ``making
an SNy-block'' is meant to deal with all deficiencies in
by invariant 5. The procedure of ``making
an SNy-block'' is meant to deal with all deficiencies in
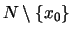 w.r.t. y in such a way that no new
deficiencies in N w.r.t. the SNy-block occur. But where we
do not take x0 into account while eliminating the deficiencies in
N w.r.t. y, we might need to take x0 into account while
eliminating the deficiencies in N w.r.t. the SNy-block.
Invariant
3 is not violated though, because it is not possible to enter the
SNy-block from y via an Sx0-successor. Therefore if
some worlds in SNy lie above x0 (and this is possible if we
eliminate a deficiency in x with x0Sx), they will not be in the
B-critical cone of x0 and hence we will not need to worry about
their B-criticality. Their successors however end up in the
B-critical cone anyway via the
w.r.t. y in such a way that no new
deficiencies in N w.r.t. the SNy-block occur. But where we
do not take x0 into account while eliminating the deficiencies in
N w.r.t. y, we might need to take x0 into account while
eliminating the deficiencies in N w.r.t. the SNy-block.
Invariant
3 is not violated though, because it is not possible to enter the
SNy-block from y via an Sx0-successor. Therefore if
some worlds in SNy lie above x0 (and this is possible if we
eliminate a deficiency in x with x0Sx), they will not be in the
B-critical cone of x0 and hence we will not need to worry about
their B-criticality. Their successors however end up in the
B-critical cone anyway via the
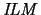 -condition (
-condition (
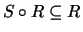 ). But this is alright, since, if
). But this is alright, since, if
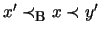 with
with 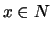 and y' in the SNy-block we automatically have
and y' in the SNy-block we automatically have
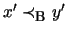 .
So at this stage of the construction we need not be
concerned about the criticality w.r.t. lower order nodes. The
procedure of ``making an SNy-block'' is now described in detail.
.
So at this stage of the construction we need not be
concerned about the criticality w.r.t. lower order nodes. The
procedure of ``making an SNy-block'' is now described in detail.
Repeat the following steps as long as deficiencies wherever in N with
respect to some element of the SNx-block exist.
The same observations as before insure the termination of this procedure.




Next: Correctness and termination
Up: The details of constructing
Previous: Making an Sxy-block.
Joost Joosten
2000-02-07