



Next: Deficiencies
Up: The construction
Previous: The construction
Easiest to deal with are the problems. Say that
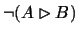 is a problem for some world m. To eliminate this problem is to
provide this m with an R-successor m' where A holds, in such a
way that from m' it is impossible to reach some world where Bholds via an Sm-transition.
As B should not hold in m' nor at any possible R-successor of m', we
should take m' to lie B critically above m.
We also must take care that starting in m'with an Sm-transition, it will never be possible to reach a world
where B holds. We should so to say ``fence the Sm-scope of m'in''. This fencing in is performed by the so-called B-critical
cone of m. We write CmB. So the whole B-critical cone of mwill lie B-critically above m, and the definition will insure that it
will not be possible to leave the B-critical cone of m with an Ror an Sm transition. By doing so, we are sure that this particular
problem
is a problem for some world m. To eliminate this problem is to
provide this m with an R-successor m' where A holds, in such a
way that from m' it is impossible to reach some world where Bholds via an Sm-transition.
As B should not hold in m' nor at any possible R-successor of m', we
should take m' to lie B critically above m.
We also must take care that starting in m'with an Sm-transition, it will never be possible to reach a world
where B holds. We should so to say ``fence the Sm-scope of m'in''. This fencing in is performed by the so-called B-critical
cone of m. We write CmB. So the whole B-critical cone of mwill lie B-critically above m, and the definition will insure that it
will not be possible to leave the B-critical cone of m with an Ror an Sm transition. By doing so, we are sure that this particular
problem
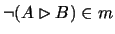 will never re-emerge.
will never re-emerge.
The existence of a B-critical successor of m containing A is
guaranteed by lemma
4.6. In our construction we
thus define this entity m' to be an Re successor of m. We write
Re instead of R because we want to be able to distinguish
essential R relations which are added to eliminate a problem, from
non-essential R relations (we write Rn) which are added either
to restore the
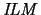 frame conditions or to eliminate
deficiencies. By R we mean the transitive closure of
frame conditions or to eliminate
deficiencies. By R we mean the transitive closure of
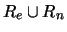 .
Sometimes we write ReB to indicate that the added Re transition is an intended B-critical one. It will turn out to be
useful to have the maximality w.r.t.
.
Sometimes we write ReB to indicate that the added Re transition is an intended B-critical one. It will turn out to be
useful to have the maximality w.r.t.  -inclusion of m'.
By this the finiteness of the construction can be guaranteed. All
the R-successors of this m' will automatically be B-critical
successors of m. It is therefore sufficient to ensure that by an
Sm-transition it is impossible to leave the B-critical cone of
m. This is incorporated in the construction and expressed by incariant
3 below.
-inclusion of m'.
By this the finiteness of the construction can be guaranteed. All
the R-successors of this m' will automatically be B-critical
successors of m. It is therefore sufficient to ensure that by an
Sm-transition it is impossible to leave the B-critical cone of
m. This is incorporated in the construction and expressed by incariant
3 below.




Next: Deficiencies
Up: The construction
Previous: The construction
Joost Joosten
2000-02-07
![]() frame conditions or to eliminate
deficiencies. By R we mean the transitive closure of
frame conditions or to eliminate
deficiencies. By R we mean the transitive closure of
![]() .
Sometimes we write ReB to indicate that the added Re transition is an intended B-critical one. It will turn out to be
useful to have the maximality w.r.t.
.
Sometimes we write ReB to indicate that the added Re transition is an intended B-critical one. It will turn out to be
useful to have the maximality w.r.t. ![]() -inclusion of m'.
By this the finiteness of the construction can be guaranteed. All
the R-successors of this m' will automatically be B-critical
successors of m. It is therefore sufficient to ensure that by an
Sm-transition it is impossible to leave the B-critical cone of
m. This is incorporated in the construction and expressed by incariant
3 below.
-inclusion of m'.
By this the finiteness of the construction can be guaranteed. All
the R-successors of this m' will automatically be B-critical
successors of m. It is therefore sufficient to ensure that by an
Sm-transition it is impossible to leave the B-critical cone of
m. This is incorporated in the construction and expressed by incariant
3 below.